Calcul de l'aire d'un cercle
(ou d'un disque)

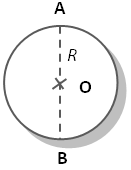
Rayon = AO = OB = R Diamètre = AB = 2 R

L’Aire A d’un cercle (ou la surface d’un cercle) est égale au produit de π (nombre pi) par la longueur du rayon R du cercle au carré :

Exemple de calcul d’une aire d’un cercle / d’un disque :

Prenons un cercle de centre O et de rayon R. Sachant que la longueur de R = 3 cm, son aire sera égale à :
Aire A = π x R² = 3,14 x 3² = 3,14 x 9 = 28,26 cm²

NB: Avec π arrondi à 3,14.

Définition d’un cercle :

Un cercle de centre O et de rayon R est l’ensemble des points du plan situé à la distance du point O. Cette distance s’appelle le rayon du cercle. Un cercle est donc défini par son centre O et son rayon R.

Définition d’un triangle isocèle :

Un triangle isocèle est un triangle dont deux côtés (au moins) ont la même longueur, et dont deux des angles sont égaux.

Définition d’un disque :

Un disque de centre O et de rayon R est l’ensemble des points du cercle et ceux intérieurs au cercle.

NB : on peut dire qu’un cercle équivaut au simple périmètre d’un disque.

Définition d’un cercle / d’un disque circonscrit dans un triangle :

Un cercle circonscrit est le cercle passant par les trois sommets d’un triangle. Son centre est situé à l’intersection des médiatrices.

Propriétés d’un cercle / d’un disque :

• - Deux points situés sur un même cercle sont situés à égale distance du centre de ce cercle.
• - Le centre d'un cercle est le milieu de tous ses diamètres. Je peux alors appliquer les mêmes propriétés que pour le milieu d'un segment
• - Si la droite T est tangente du cercle en un point F, alors (T) est perpendiculaire au rayon OF (ou diamètre EF)
• - et la propriété inverse : Si une droite est perpendiculaire à un rayon du cercle en un point du cercle, alors cette droite est appelée tangente de ce cercle.

Pour aller plus loin :

• - Calculer le périmètre d'un cercle (c’est-à-dire la longueur du tour d’un disque)
• - Calculer le volume d’une sphère