Calcul du volume d'une sphère

Le volume d’une sphère est égal au produit de 4/3 par π (nombre pi environ égal à 3,14) par son rayon au cube :

Volume d'une sphère =

Longueur du rayon r (en unité : cm, m…) :
Volume de la sphère (en unité 3) :

Exemple de calcul du volume d’une sphère :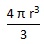

Soit une sphère de rayon r = 3 cm

Volume V = 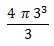= 113,04 cm3

Définition d’une sphère :

Une sphère est une surface à 3 dimensions dont tous les points sont situés à une même distance d'un point appelé centre. La valeur de cette distance commune au centre est appelée le rayon de la sphère. Elle n'inclut donc pas les points situés à une distance inférieure au rayon, au contraire de la boule. Concrètement, on peut voir une sphère comme une coquille vide infiniment mince.

Une sphère peut aussi être définie comme la surface formée par la rotation d'un cercle autour de son diamètre.

Exemple d’une sphère : une balle de tennis

Propriétés de la sphère :

  • - La sphère de centre O et de rayon r est l'ensemble des points de l'espace dont la distance à O est égale à r.
  • - Le rayon est un segment délimité par le centre et un point de la sphère.
  • - La longueur du rayon est la distance entre le centre de la sphère n'importe quel point de la sphère.
  • - Le diamètre est un segment de droite passant par le centre et limité par les points de la sphère.
  • - La longueur du diamètre est égale à la longueur du rayon multipliée par 2.
  • - Toute droite passant par le centre d'une sphère coupe celle-ci en deux points diamétralement opposés.

Important :

Une sphère est l’extérieur / la surface d’une boule.

Autrement dit, on calcul l’aire d’une sphère, mais le volume d’une boule.

Pour reprendre l’image de la balle de tennis, cette dernière est en fait une coquille vide, donc une sphère, et l’intérieur en est la boule.

Pour aller plus loin :